Calculating the Instantaneous Axis of Rotation
The instantaneous axis of rotation between two bodies is a useful concept in biomechanics.
In this post, we will dig into how to calculate the instantaneous
axis of rotation and show an AnyScript class_template that calculate and displays the
axis between any two reference frames in the AnyBody
Modeling System.
Before we dive into the AnyScript implementation let us look briefly at the math behind the instantaneous axis of rotation.
Rigid body motion in 3D
We can view any displacement of a body in a three-dimensional space as a rotation around a single axis and a translation along that axis. This gives rise to the idea of a screw motion in 3D along what is also called the helical axis. If we split the movement up into infinitesimally small movements each of these will have an rotation axis and a linear velocity along that axis. This is the instantaneous axis of rotation, and as the name indicate will change direction and location as the object moves.
The angular velocity of rigid body is a vector quantity shared by all point of the rigid body. My old engineering math book defines it from the rate of change of the rotation matrix \(R\):
\[\frac{ {\mathrm d} }{ {\mathrm d}t}R = \vec{\omega} \times R\]If we know the angular and linear velocity of any point on a rigid body, we can calculate the properties of the screw motion and the instantaneous axis of rotation.
Using\(\vec{\omega}\)we can write the velocity \(\vec{v}_P\) of a point \(P\) at some distance \(\vec{r}\) from the instantaneous axis of rotation as a sum of the linear velocity \(\vec{v}_C\) along the axis of rotation and the tangential velocity around the axis of rotation:
\[\begin{equation} \label{eq:1} \vec{v}_P = \vec{v}_C + \vec{\omega} \times \vec{r} \end{equation}\]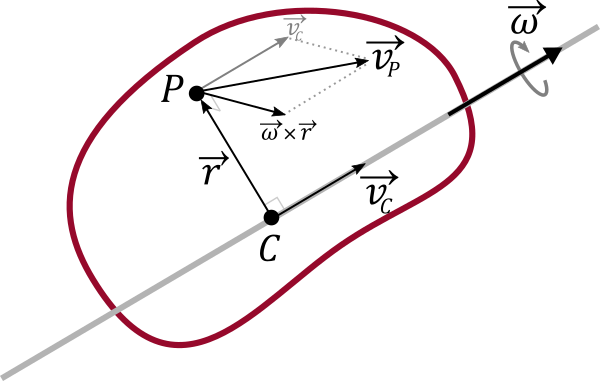
Similarly we can also calculate backwards and find the intantanous axis of rotation at some distance \(-\vec{r}\) from any point if we know the linear velocity of the point and the angular velocity. This is given by:
\[\begin{equation} \label{eq:2} -\vec{r}= \frac{\vec{\omega} \times \vec{v}_P }{ \vec{\omega}\cdot\vec{\omega} } \end{equation}\]Thus if know the position of a point \(\vec{r}_P\), its linear velocity \(\vec{v}_P\) we can find closest point $\vec{r}_C$ on the rotation axis as:
\[\vec{r}_C = \vec{r}_P - \vec{r} = \vec{r}_P + \frac{\vec{\omega}\times\vec{v}_P}{\vec{\omega}\cdot\vec{\omega} }\]Short proof of \(\eqref{eq:2}\), skip it if you like:
Start with \(\vec{\omega} \times \vec{v}_P\) and insert \(\eqref{eq:1}\). Since \(\vec{\omega}\) and \(\vec{v}_C\) are parallel their cross product cancel out.
\[\require{cancel} \vec{\omega} \times \vec{v}_P = \vec{\omega} \times (\vec{v}_C+\vec{\omega} \times \vec{r})= \cancel{\vec{\omega} \times \vec{v}_C}+\vec{\omega}\times (\vec{\omega} \times \vec{r})\]Next we use the vector tripple product to expand, and we note that \(\vec{\omega}\cdot\vec{r}\) cancel out since the shortest vector from the rotation axis to any point is always perpendicular to angular velocity:
\[\require{cancel}\vec{\omega}\times (\vec{\omega} \times \vec{r}) = \vec{\omega}(\cancel{\vec{\omega}\cdot\vec{r} })-\vec{r}(\vec{\omega}\cdot\vec{\omega})\]Finally we have:
\[\vec{\omega} \times \vec{v}_P = -\vec{r}(\vec{\omega}\cdot\vec{\omega}) \Leftrightarrow -\vec{r}= \frac{\vec{\omega} \times \vec{v}_P }{ \vec{\omega}\cdot\vec{\omega} }\]Disclaimer:
The math may not be strictly accurate. Sorry, I am an Engineer :) If you have more math skill than I please help make this more concise.
Properties
If for example, we have a rigid body with angular velocity \(\vec{\omega}\) and some point \(P\) with position \(\vec{r}_P\) and velocity \(\vec{v}_p\) then we can define the different properties:
| Quantity | Description |
|---|---|
| \(\omega = |\vec{\omega}|\) | The magnitude of angular rotation. |
| \(\vec{e}_{IOAR} = \frac{\vec{\omega} }{\omega}\) | The direction of the intantanous axis of rotation. |
| \(\vec{r}_C = \vec{r}_P + \frac{\vec{\omega}\times\vec{v}_P}{\vec{\omega}\cdot\vec{\omega} }\) | The point C on the intantanous axis of rotation. |
| \(h = \frac{\vec{\omega} \cdot \vec{v}_P}{\vec{\omega}\cdot\vec{\omega} }\) | Ratio of angular to linear angular velocity |
| \(\vec{v}_C = h\vec{\omega}\) | The linear velocity at point \(C\) along the axis of rotation. |
The list of properties is inspired by this answer from StackExchange Physics
All we need to know is the rotation velocity of a body and the velocity of any point to find the instantaneous axis of rotation.
AnyScript implementation
In AnyScript we can easily find the angular velocity, and the linear velocity of
a reference frame using the two classes AnyKinRotational and AnyKinLinear.
An implementaion to find the instantanous axis of rotation could be as simple as:
AnyKinRotational Rotational ={
AngVelOnOff = On;
AnyRefFrame& Ref1= .ReferenceFrame;
};
AnyKinLinear Linear ={
Ref=-1;
AnyRefFrame& Ref1= .ReferenceFrame;
};
/// Direction of the instantaneous axis of rotation
AnyVec3 e_iaor = Rotational.Vel/vnorm(Rotational.Vel)
/// The point on the rotation axis closest to ReferenceFrame origin
AnyVec3 r_iaor = Linear.Pos + cross(Rotational.Vel, Linear.Vel)/(vnorm(Rotational.Vel)^2);It is important to set AngVelOnOff = On; to make AnyKinRotational output the
angular velocity vector. Of course this the code above is very simplified. We
would also like a way to find the axis between between two moving bodies, and
also draw the axis in the process.
AnyScript class template
We have created a custom class template that makes it easy to calculate the properties listed above and display the instantaneous axis of rotation. Here is a short example on how to use the class:
#include "path/to/InstantaneousAxisOfRotation.any"
Main = {
InstantaneousAxisOfRotation IAOR (
Body1 = .Segments.Ground,
Body2 = .Segments.Ball
) = { };That is all it takes. Here a how it looks for few very simple models:
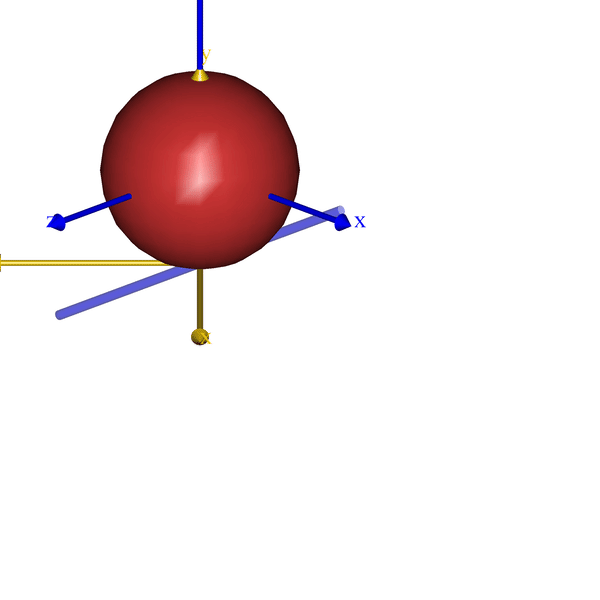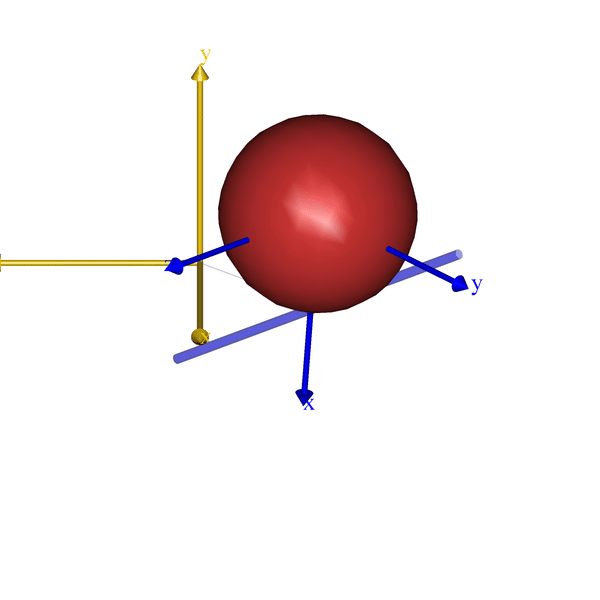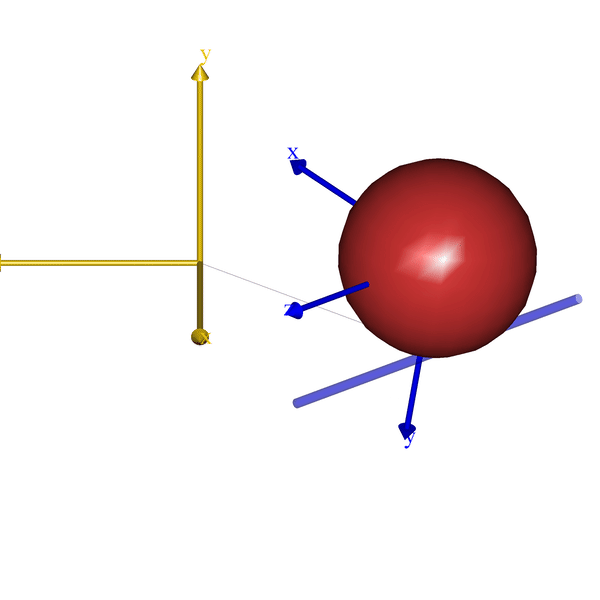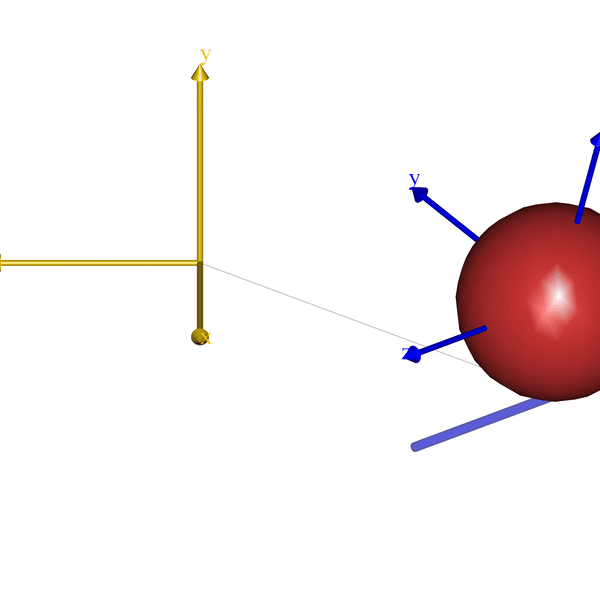
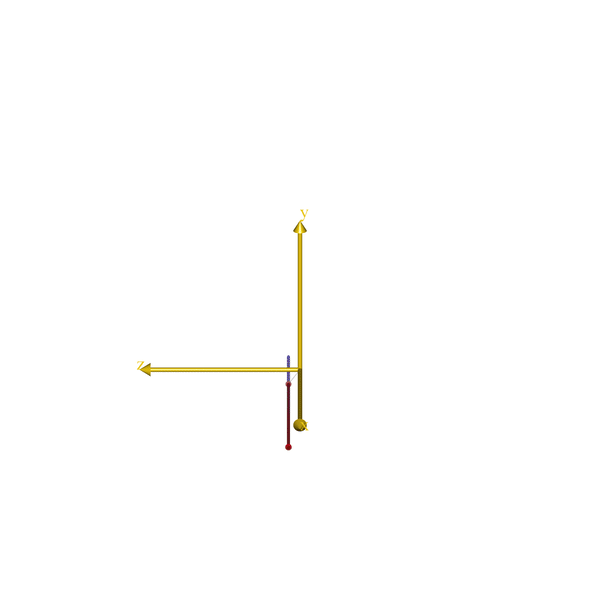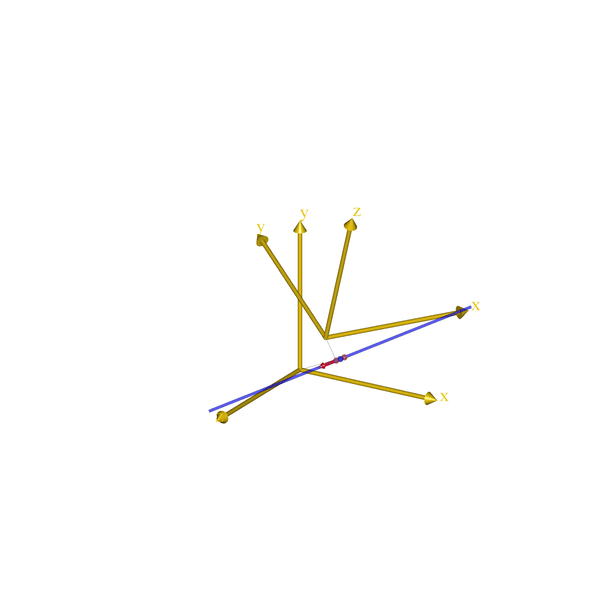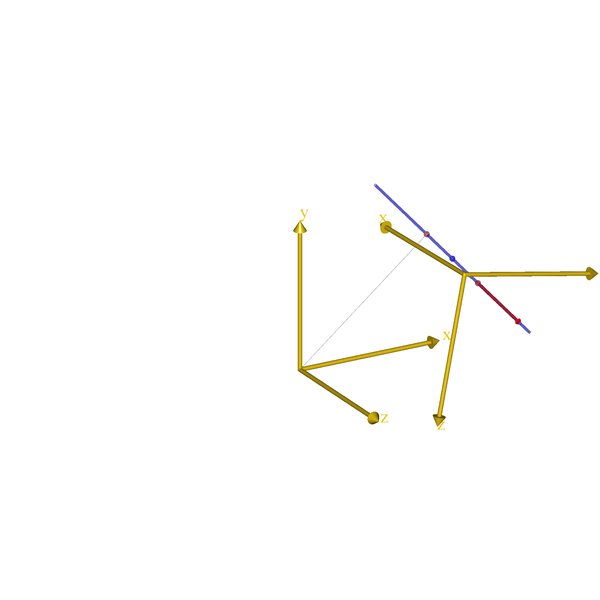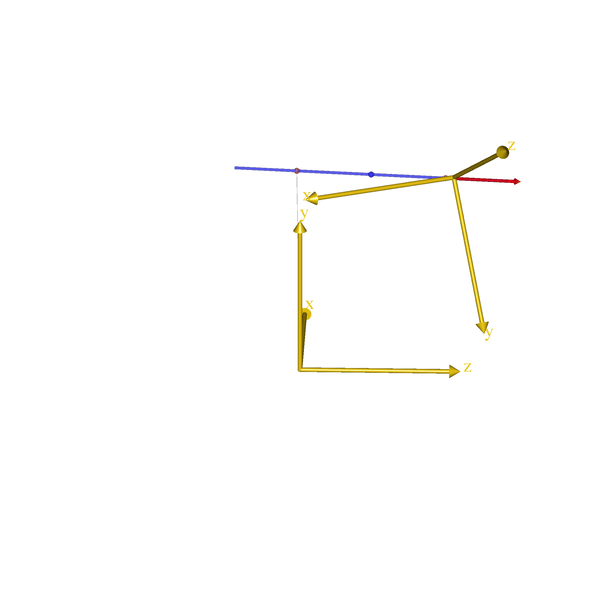
The code will eventually become part of the AnyBody Managed Model Repository (AMMR), which is shipped with the AnyBody Modeling System. But until the next release of the AMMR, the class template can be downloaded from GitHub.


Leave a comment