Lesson1: Mechanical System Information

This lesson assumes that you have the arm2d.any file ready in AnyBody. If you do not have the model on your computer, please get and save a copy from this link: arm2d.any. It should look like this when you have loaded the model, run InitialConditions operation, and opened a Model View:

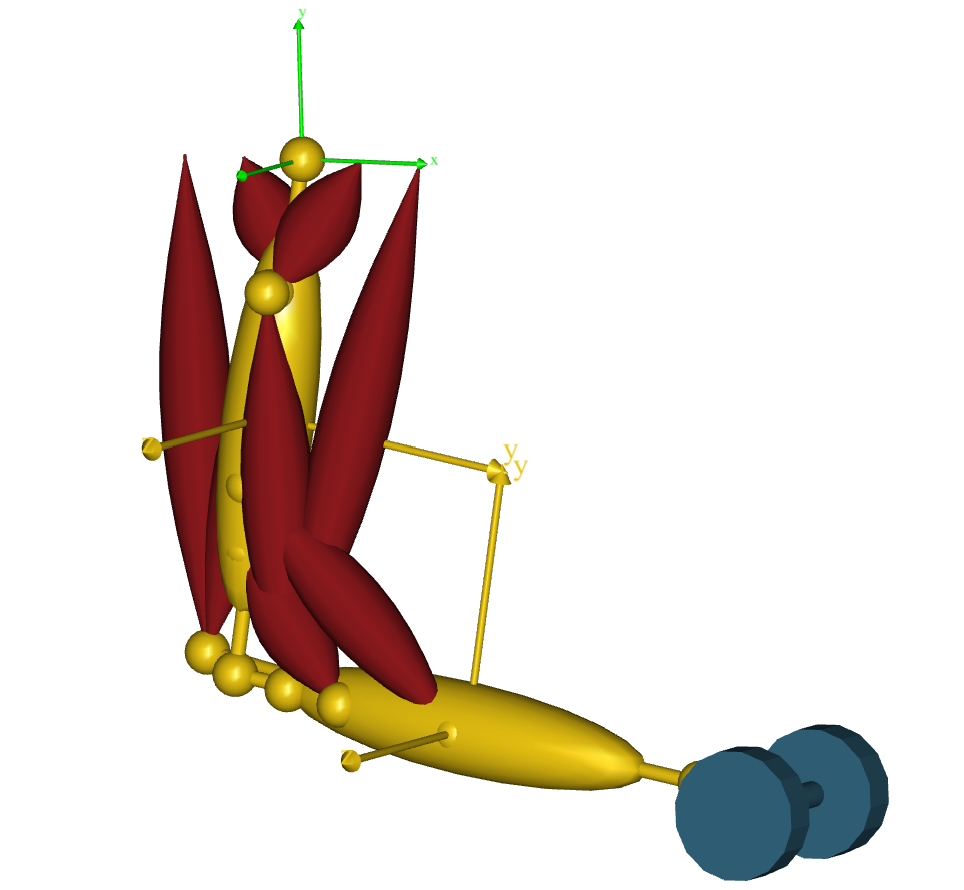
This model is relatively simple in how it works, because it only has two parts and two rotating joints. But, in more complex models with many parts joined by different kinds of joints, it can be hard to keep track of the model. To make a model move, you need to balance the kinematic degrees of freedom and the constraints, and this can be challenging to do perfectly.

Mechanical studies have a description of the mechanical system. You can find this in the “Objects Description” of the study, which you can see by double-clicking the objects in any Model Tree View. If you double-click the ArmModel study folder in the model that is loaded, you will see a System description like this:

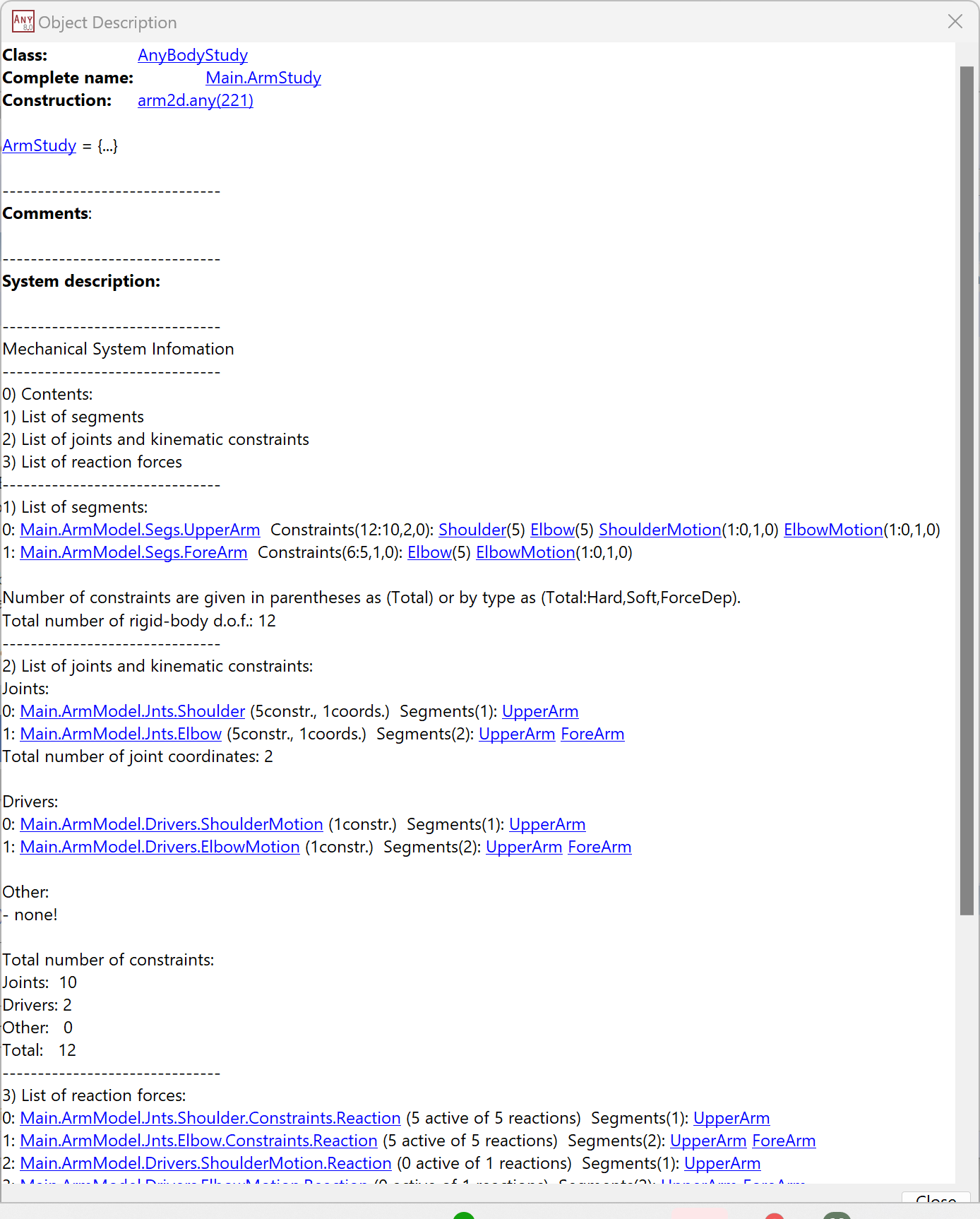
The Mechanical System Information consists of four parts:

For a simple model like “arm2d” where all the segments are next to each other, it may seem excessive to list them all, but bigger models usually have the segment definitions spread over many different folders and files, and it can be useful to see a combined list of all of them.

AnyBody models are 3D, with each rigid segment having six degrees of freedom (3 translational movements and 3 rotations). Thus, the “Mechanical System Information” multiplies the segment count by 6 to get the total degrees of freedom, which is 12 in this case.

To locate everything in space, we need 12 constraints, which is the role of section 2 in the Mechanical System Information. This section tallies the kinematic constraints, which must equal the model’s degrees of freedom for the system to be kinematically determined, i.e., 12 constraints for this model.

The 12 constraints are derived from the two revolute joints in the model for the shoulder and elbow. A revolute joint retains one degree of freedom between the two reference frames it links, resulting in five constraints. With two joints, we have two degrees of freedom left (12 - 2 x 5 = 2), also known as the joint coordinates. The remaining section must specify this number of additional constraints.

Drivers

A common way of containing the movement of the joints is by using drivers. As the list shows, we have done that by adding two drivers to the two joints in our case. But that is not the only option. We need to have as many constraints as we have joint coordinates, but the contraints do not have to target the joint coordinates directly. For example, we could have also driven the x and y coordinates of a point on the lower arm.

Another section is called “Other:”. This is for constraints that are not one of the predefined joint types or driver functions. These constraints are common in more complex models because the AnyScript language lets users create their own joints and other constraints to simulate complex movements patterns between different joints. But this is an advanced topic that we will leave for later.

Reaction forces

The last section 3 shows the reaction forces. It is not by chance that the reaction and driver forces have the same total as the joints and kinematic constraints.

In a simple model like this one, the number of reactions from joints is usually equal to the number of kinematic constraints. This reflects most real-life situations, because the mechanical joints we encounter in our environment apply their kinematic constraints through reaction forces. But the body is not always like that. For example, a knee can be roughly modeled as a hinge joint (many physiologists will object here) but the internal mechanisms that carry loads in the knee are not like those in a mechanical hinge. Instead, knee reactions result from a complex combination of unilateral joint surfaces, ligaments, and muscles.

See also

For an in-depth discussion of some of these issues, please refer to the tutorial on mechanical elements.

So AnyBody allows for the creation of joints that only have kinematic constraints but not the corresponding reaction forces. In fact, the system also allows the opposite: Reaction forces without kinematic constraints.

Important

The main point for now is that it can be difficult to count reactions at times, and the Object Description’s “Mechanical System Information” can help with this.

A few special cases are:

1. The number of reaction and driver forces is lower than the number of degrees of freedom for the rigid bodies in the model, which happens here. This means that some reactions need to come from other elements, and these elements are usually the muscles in the model.

2. If the number of reaction and driver forces matches the number of degrees of freedom for the rigid bodies, then the model can usually balance itself, and there is no need for muscles. In fact, if you add muscles to such a mechanism, the muscles will not do anything.

3. If the model has more reaction and driver forces than degrees of freedom for the rigid bodies, then it is statically indeterminate. This usually indicates that there is something wrong with the model. Mechanically it means that the model has multiple different ways of balancing itself and cannot decide which one is correct. Even though AnyBody can calculate the forces in such a model, you will often see the solutions fluctuating between the infinitely many options between time steps. Models like these should generally be avoided.

Exercises

We will explore the effects of modifying the model. We will start by taking out one of the drivers in the model, making it kinematically indeterminate:

AnyFolder Drivers = {

      //---------------------------------
//     AnyKinMotion ShoulderMotion = {
//         AnyRevoluteJoint &Jnt = ..Jnts.Shoulder;
//         DriverPos0 = {-100*pi/180};
//         DriverVel0 = {30*pi/180};
//      }; // Shoulder driver
      
      //---------------------------------
      AnyKinMotion ElbowMotion = {
         AnyRevoluteJoint &Jnt = ..Jnts.Elbow;
         DriverPos0 = {90*pi/180};
         DriverVel0 = {45*pi/180};
      }; // Elbow driver
   }; // Driver folder

When you load the model again, you will get this message:

Model Warning: Study 'Main.ArmStudy' contains too few kinematic constraints to be kinematically determinate.

This means that when you load the model, the system automatically detects that there might be too few kinematic constraints for the model. This can make it impossible to assemble the mechanism and very unlikely to run a kinematic analysis. If you double-click the ArmStudy folder to open the Object Description window, you will see this output:

The Mechanical System Information lets you examine closely how many constraints are not there and what kind they might be. Let us move the missing driver back into place:

//---------------------------------
AnyKinMotion ShoulderMotion = {
  AnyRevoluteJoint &Jnt = ..Jnts.Shoulder;
  DriverPos0 = {-100*pi/180};
  DriverVel0 = {30*pi/180};
}; // Shoulder driver

//---------------------------------
AnyKinMotion ElbowMotion = {
  AnyRevoluteJoint &Jnt = ..Jnts.Elbow;
  DriverPos0 = {90*pi/180};
  DriverVel0 = {45*pi/180};
}; // Elbow driver

… and try something else:

//---------------------------------
AnyKinMotion ShoulderMotion = {
  AnyRevoluteJoint &Jnt = ..Jnts.Shoulder;
  DriverPos0 = {-100*pi/180};
  DriverVel0 = {30*pi/180};
}; // Shoulder driver

//---------------------------------
AnyKinMotion ElbowMotion = {
  AnyRevoluteJoint &Jnt = ..Jnts.Elbow;
  DriverPos0 = {90*pi/180};
  DriverVel0 = {45*pi/180};
}; // Elbow driver

AnyReacForce ExtraReactionForces = {
  AnyRevoluteJoint &Jnt1 = ..Jnts.Shoulder;
  AnyRevoluteJoint &Jnt2 = ..Jnts.Elbow;
};

Here, we have added extra reaction forces to the two joints. This is like putting motors into the joints, and it means that the system will get enough reaction forces to support the loads without needing any muscles, which matches the statically determinate case 2 above. Loading the model does not cause any warnings, but if you run the InverseDynamics operation you will see the following message.

WARNING(OBJ.MCH.MUS1) :   arm2d.any(227)  :   ArmStudy  :  The muscles in the model are not loaded due to kinetically over-constrained mechanical system.

And the Object Description window will give the following feedback:

indicating that the model is precisely statically determinate with 12 reactions corresponding to the 12 rigid body degrees of freedom.

Now that we have learned about the Mechanical System Information in the Object Description of the study, we can move on to Initial Conditions in the next lesson.