Inverse Dynamics of Muscle Systems#
The AnyBody Modeling System performs inverse dynamics as one of its central operations. In biomechanics, inverse dynamics is traditionally understood as the process of computing from measured ground reaction forces in a gait analysis to net moments in the anatomical joints.
At least in AnyBody context, inverse dynamics is much more than that. In brief, inverse dynamics allows you to simulate muscle and joint forces in the entire body undergoing complex movements, taking dynamic inertia forces into account, and not necessarily requiring measured forces in the interface between the body and the environment. Inverse dynamics had the advantage that it allows for analysis of very complicated musculoskeletal systems comprising hundreds of muscles on desktop or laptop computers in a few seconds.
The figure below illustrates the simple principle behind inverse dynamics.
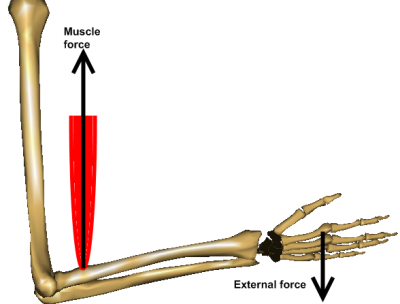
If we know the magnitude of the external force, and we know the length of the forearm and the insertion point of the biceps muscle on the forearm, then it is not difficult to compute the muscle force from simple moment equilibrium about the elbow. Further equilibrium equations can subsequently give us the reaction forces in the elbow joint.
This is really the principle of inverse dynamics as it takes place in the AnyBody Modeling System. So why do we need to make these computations with advanced software? Well, there are several complications that make realistic cases somewhat more challenging. The figure below illustrates some of them.
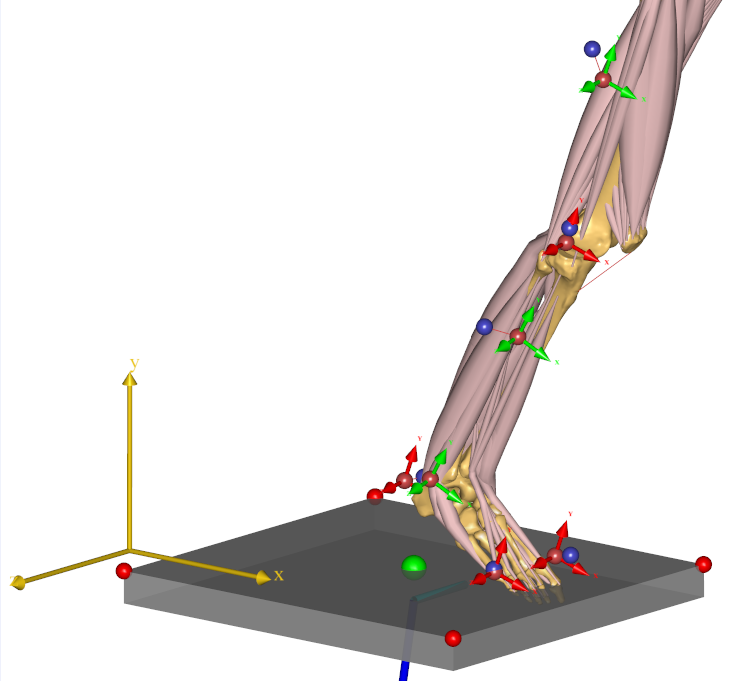
This figure is a much more anatomically realistic representation of the mechanics of a human upper extremity. Even if we count only from the gleno-humeral joint to the wrist, thus disregarding the shoulder girdle and the hand, the arm will have seven independent degrees of freedom, i.e. seven different joint articulations, and not just one, as we implicitly assumed in the simple examples before. Moreover, many more muscles than the single biceps from the previous figure are involved in flexing the elbow, and many of these muscles span several joints. It even turns out that some of the muscles will end up working antagonistically, i.e. against each other. The multiple degrees of freedom and multiple muscles directly lead to a much larger system of equilibrium equations that have to be formulated and solved, and this is not something that can be done easily by hand.
Another complication is that many muscles are wrapping over bones on their way from origin to insertion. This complicates the mechanics of the problem significantly because the muscle path is not easy to predict and because the muscle provides force to the bone it is wrapping over and not just at its origin and insertion points.
For obvious graphical reasons, the figure shown here does not move as living bodies usually do. Movement also complicates the case significantly by adding inertia forces to the problem and by changing the equilibrium equations from one time step to the next. The bottom line is that it is virtually impossible to simulate realistic musculoskeletal systems “by hand” or even develop them bottom-up by general mathematical software. The only viable solution is to use a computer system designed for this particular purpose, so here we are. With the AnyBody Modeling System you can easily define very complex musculoskeletal systems and analyze them dynamically as you have probably already done in the Getting Started tutorial. If not, now would be a good time to do it and familiarize yourself with the mouse clicks necessary to conduct the InverseDynamics operation and inspect the results before continuing with the next steps of this tutorial.
There is one more complexity that has not been mentioned yet: The body has many more muscles than strictly necessary to balance its degrees of freedom, and this means that there are infinitely many different ways the body can recruit its muscles to get the job done. The understanding of this problem and how it is dealt with in the AnyBody Modeling System is so important that the rest of this tutorial is dedicated to the problem. We are going to take a deductive approach because it is necessary for a reasonable understanding of the physiological assumptions behind the entire field of muscle recruitment. More on this topic can be found in the recorded previous webcast on “Features of muscle recruitment algorithms“.
Let us begin with Lesson 1: The basics of muscle recruitment.